Lecture 2. B) Leibniz Rule
Leibniz Rule
This rule can be useful in a series of domains. It states that
[math]\frac{d}{dx}\int_{a\left(x\right)}^{b\left(x\right)}f\left(x,t\right)dt=\int_{a\left(x\right)}^{b\left(x\right)}\frac{\partial}{\partial x}f\left(x,t\right)dt+f\left(x,b\left(x\right)\right)b'\left(x\right)-f\left(x,a\left(x\right)\right)a'\left(x\right).[/math]
This means that the derivative of an integral can written as the integral of a derivative, plus functions of the integrands and of the integration limits. The case where [math]b\left(x\right)[/math] and [math]a\left(x\right)[/math] are constant follows immediately.
For this rule to apply, we require [math]f\left(x,t\right)[/math] and its partial derivative w.r.t. [math]x[/math] to be continuous, and that both limits of integration are continuously differentiable. We also note that this rule can be derived from the chain rule of differentiation (see this proof).
Improper Integrals
When the integral is improper (i.e., one of the limits is infinity), Leibniz rule may fail despite all relevant functions being otherwise well-behaved.
At the crux of this problem is whether [math]\lim_{h\rightarrow0}\int_{0}^{\infty}\frac{f\left(x+h,t\right)-f\left(x,t\right)}{h}dt=\int_{0}^{\infty}\lim_{h\rightarrow0}\frac{f\left(x+h,t\right)-f\left(x,t\right)}{h}dt[/math].
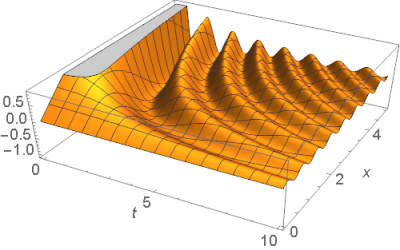
Consider the example of the following function:
[math]f\left(x,t\right)=\frac{\sin\left(tx\right)}{t},[/math]
plotted below:
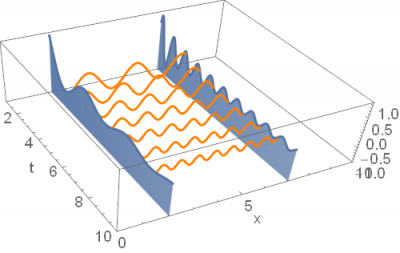
First, notice that by calculating the expression of interest directly, [math]\frac{d}{dx}\int_{0}^{\infty}f\left(x,t\right)dt[/math], we learn how the area under [math]f\left(x,t\right)[/math] along the [math]t[/math] axis changes when [math]x[/math] is moved slightly. In order to see this, consider the following plot of [math]\frac{\sin\left(tx\right)}{t}[/math], shown now only for specific values of [math]t[/math] and [math]x[/math].
For now, we will focus on the blue sections, along which [math]x[/math] is fixed. We can think of [math]\frac{d}{dx}\int_{0}^{\infty}f\left(x,t\right)dt[/math] as first calculating the area under each of the blue curves, and then calculating how those areas change as a function of [math]x[/math]. By calculating this expression directly, we obtain
[math]\frac{d}{dx}\int_{0}^{\infty}f\left(x,t\right)dt=\frac{d}{dx}\frac{\pi}{2}sign\left(x\right),[/math]
which equals zero at [math]x\neq0[/math] and is infinite at [math]x=0[/math]. This is the correct answer: As [math]x[/math] changes slightly, the area under [math]f\left(x,t\right)[/math] remains constant, except at [math]x=0[/math], where it changes at an infinite rate.
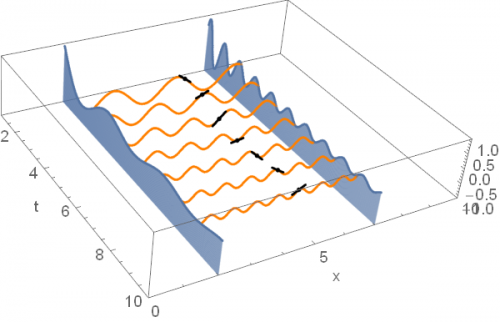
Now, consider the alternative calculation, [math]\int_{0}^{\infty}\frac{\partial}{\partial x}f\left(x,t\right)dt[/math]. In this case, we first calculate how much the function changes with small increments in [math]x[/math] for generic values of [math]t[/math]. For example, we could be calculating the vertical differences in the endpoints of the orange lines of the plot above. Then, we add up these differences along [math]t[/math], by applying the integral.
The integrand of this expression is given by: [math]\frac{\partial}{\partial x}f\left(x,t\right)=\frac{\partial}{\partial x}\frac{\sin\left(tx\right)}{t}=\text{cos}\left(tx\right)[/math]. We have learned that the slope of [math]f[/math] along the [math]x[/math]-axis is periodic. Function [math]\text{cos}\left(tx\right)[/math] represents the information about the slopes, which we represent below through small line segments, along [math]x=5[/math]:
A property of the cosine (and other elementary trigonometric functions) is that, for a given [math]x[/math], the area 'underneath' is also periodic and does not vanish as we approximate infinity. This is a problem: When we take an integral from zero to infinity, the area under [math]\text{cos}\left(tx\right)[/math] does not converge.
Intuitively, the integral adds up the slopes in the [math]x[/math] direction, which keep rotating forever. If these slopes stabilized at some point (for example, if they all approximated zero when [math]t[/math] was large), then the integral would also converge. However, because the slopes keep rotating as [math]t[/math] changes, the integral does not converge and Leibniz rule fails. This issue can only arise when at least one of the limits of integration is infinity.
When this issue does not apply (i.e., the integral of the partial derivative converges), then result
[math]\frac{d}{dx}\int_{a\left(x\right)}^{b\left(x\right)}f\left(x,t\right)dt=\int_{a\left(x\right)}^{b\left(x\right)}\frac{\partial}{\partial x}f\left(x,t\right)dt+f\left(x,b\left(x\right)\right)b'\left(x\right)-f\left(x,a\left(x\right)\right)a'\left(x\right)[/math]
is valid. If [math]a\left(x\right)=\infty[/math] or [math]b\left(x\right)=\infty[/math], we apply identity [math]\frac{d\infty}{dx}=0[/math], thus ignoring the latter terms of the expression.
- For an alternative intuition, see Lecture 2. B) Leibniz Rule II.