Lecture 16. B) Example: Coin Tossing
Example: Coin Tossing
- Likelihood: [math]f\left(\left.x\right|p\right)=p^{x}\left(1-p\right)^{1-x}1\left(x\in\left\{ 0,1\right\} \right)[/math]
- Prior Belief: [math]f\left(p\right)=1\left(p\in\left[0,1\right]\right)[/math]
- Joint Distribution: [math]f\left(x,p\right)=f\left(\left.x\right|p\right)f\left(p\right)=p^{x}\left(1-p\right)^{1-x}[/math]
- Marginal distribution of [math]X[/math]:
[math]\begin{aligned} f\left(x\right) & =\int_{p\in\left[0,1\right]}f\left(\left.x\right|p\right)f\left(p\right)dp\\ & =\int_{p\in\left[0,1\right]}f\left(x,p\right)dp\\ & =\int_{0}^{1}p^{x}\left(1-p\right)^{1-x}dp\\ & =\frac{1}{2},\,for\,x\in\left\{ 0,1\right\} .\end{aligned}[/math]
(The integral above is especially complicated; you don’t need to know how to solve it on your own; however, if you notice that we only need its value at [math]x\in\left\{ 0,1\right\} ,[/math] then one can replace the integrand by [math]px+\left(1-p\right)\left(1-x\right)[/math] and obtain the same result.)
So,
[math]f\left(\left.p\right|x\right)=\frac{p^{x}\left(1-p\right)^{1-x}}{\frac{1}{2}}=2p^{x}\left(1-p\right)^{1-x}.[/math]
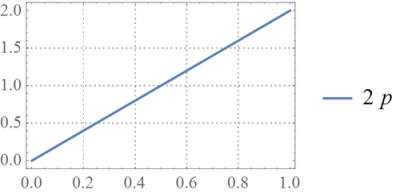
To see how this posterior depends on data, consider the case where we observe [math]x=1[/math]. Then, [math]f\left(\left.p\right|1\right)=2p[/math], and our estimate for [math]p[/math] may be
[math]\left(\left.\widehat{p}\right|X=1\right)=E\left(\left.p\right|X=1\right)=\int_{0}^{1}p2pdp=\left.\frac{2}{3}p^{3}\right|_{0}^{1}=\frac{2}{3}.[/math]
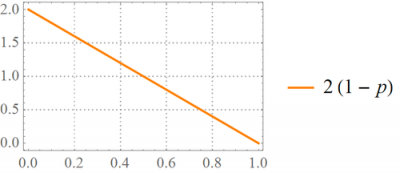
Now, suppose we observe [math]x=0[/math]. Then, [math]f\left(\left.p\right|1\right)=2\left(1-p\right)[/math], and our estimate for [math]p[/math] becomes
[math]\left(\left.\widehat{p}\right|X=0\right)=E\left(\left.p\right|X=0\right)=\int_{0}^{1}p2\left(1-p\right)dp=\left.2\left(\frac{p^{2}}{2}-\frac{p^{3}}{3}\right)\right|_{0}^{1}=\frac{1}{3}.[/math]
As expected, the point estimate for [math]p[/math] increases with [math]X[/math] .
Below, see the posterior pdfs of [math]p[/math] for [math]x=0[/math] and [math]x=1[/math]:
The posterior probability of [math]p[/math] is higher for higher values of [math]p[/math] when [math]x=1[/math], but it is lower for high values of [math]p[/math] when [math]x=0[/math].