Full Lecture 16
Contents
Bayesian Inference
In the classical approach, a probability is regarded as a long run frequency/propensity. We take random samples from a population of infinite size, and parameter [math]\theta[/math] is fixed.
In the Bayesian approach, a probability is a subjective degree of belief. Parameters themselves are regarded as random, and beliefs are updated based on data.
Ingredients
- Model for the data given some known parameters, [math]f_{\left.X\right|p}\left(\left.x\right|p\right)[/math].
- Prior distribution of parameters, [math]f_{p}\left(p\right)[/math].
- Bayes Theorem: [math]\underset{\text{posterior distribution}}{\underbrace{f_{\left.p\right|X}\left(\left.p\right|x\right)}}=\frac{f_{X,p}\left(X,p\right)}{f_{X}\left(x\right)}=\frac{\overset{\text{likelihood function}}{\overbrace{f_{\left.X\right|p}\left(\left.x\right|p\right)}}.\overset{\text{prior distribution}}{\overbrace{f_{p}\left(p\right)}}}{\int f_{\left.X\right|p}\left(\left.x\right|p\right)f_{p}\left(p\right)dp}[/math]
In this framework, estimating a parameter means finding [math]f_{\left.p\right|X}[/math] for some data [math]x_{1}..x_{n}[/math]. Unlike in the classical approach, parameters are now distributed according to function [math]f_{p}\left(\cdot\right)[/math], although we’ll keep writing them in lowercase. In actual estimation, this function may encompass the researcher’s past experience or data from previous experiments. In practice, the function is often chosen to be relatively uninformative.
The posterior distribution is the updated distribution of the parameters, conditional on data. We may use the distribution to generate point estimates (by taking expectations of the parameters, for example).
Example: Coin Tossing
- Likelihood: [math]f\left(\left.x\right|p\right)=p^{x}\left(1-p\right)^{1-x}1\left(x\in\left\{ 0,1\right\} \right)[/math]
- Prior Belief: [math]f\left(p\right)=1\left(p\in\left[0,1\right]\right)[/math]
- Joint Distribution: [math]f\left(x,p\right)=f\left(\left.x\right|p\right)f\left(p\right)=p^{x}\left(1-p\right)^{1-x}[/math]
- Marginal distribution of [math]X[/math]:
[math]\begin{aligned} f\left(x\right) & =\int_{p\in\left[0,1\right]}f\left(\left.x\right|p\right)f\left(p\right)dp\\ & =\int_{p\in\left[0,1\right]}f\left(x,p\right)dp\\ & =\int_{0}^{1}p^{x}\left(1-p\right)^{1-x}dp\\ & =\frac{1}{2},\,for\,x\in\left\{ 0,1\right\} .\end{aligned}[/math]
(The integral above is especially complicated; you don’t need to know how to solve it on your own; however, if you notice that we only need its value at [math]x\in\left\{ 0,1\right\} ,[/math] then one can replace the integrand by [math]px+\left(1-p\right)\left(1-x\right)[/math] and obtain the same result.)
So,
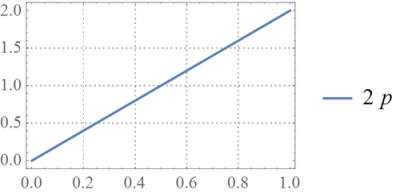
[math]f\left(\left.p\right|x\right)=\frac{p^{x}\left(1-p\right)^{1-x}}{\frac{1}{2}}=2p^{x}\left(1-p\right)^{1-x}.[/math]
To see how this posterior depends on data, consider the case where we observe [math]x=1[/math]. Then, [math]f\left(\left.p\right|1\right)=2p[/math], and our estimate for [math]p[/math] may be
[math]\left(\left.\widehat{p}\right|X=1\right)=E\left(\left.p\right|X=1\right)=\int_{0}^{1}p2pdp=\left.\frac{2}{3}p^{3}\right|_{0}^{1}=\frac{2}{3}.[/math]
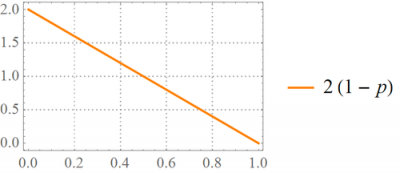
Now, suppose we observe [math]x=0[/math]. Then, [math]f\left(\left.p\right|1\right)=2\left(1-p\right)[/math], and our estimate for [math]p[/math] becomes
[math]\left(\left.\widehat{p}\right|X=0\right)=E\left(\left.p\right|X=0\right)=\int_{0}^{1}p2\left(1-p\right)dp=\left.2\left(\frac{p^{2}}{2}-\frac{p^{3}}{3}\right)\right|_{0}^{1}=\frac{1}{3}.[/math]
As expected, the point estimate for [math]p[/math] increases with [math]X[/math] .
Below, see the posterior pdfs of [math]p[/math] for [math]x=0[/math] and [math]x=1[/math]:
The posterior probability of [math]p[/math] is higher for higher values of [math]p[/math] when [math]x=1[/math], but it is lower for high values of [math]p[/math] when [math]x=0[/math].
A more general example
- Likelihood: [math]f\left(\left.x\right|p\right)=p^{x}\left(1-p\right)^{1-x}1\left(x\in\left\{ 0,1\right\} \right)[/math], before.
- Prior Belief: [math]f\left(p\right)=Beta\left(\alpha,\beta\right)=\frac{\Gamma\left(\alpha+\beta\right)}{\Gamma\left(\alpha\right)\Gamma\left(\beta\right)}p^{\alpha-1}\left(1-p\right)^{\beta-1}[/math]. (note that [math]Beta\left(1,1\right)=U\left(0,1\right).[/math])
Recall that [math]E\left(p\right)=\frac{\alpha}{\alpha+\beta}[/math] and [math]Var\left(p\right)=\frac{\alpha\beta}{\left(\alpha+\beta\right)^{2}\left(1+\alpha+\beta\right)}[/math].
The posterior probability when [math]x=1[/math] is given by:
[math]f\left(\left.p\right|x=1\right)=\frac{\frac{\Gamma\left(\alpha+\beta\right)}{\Gamma\left(\alpha\right)\Gamma\left(\beta\right)}p^{\alpha-1}\left(1-p\right)^{\beta-1}p}{f_{X}\left(1\right)=\int_{0}^{1}f_{\left.X\right|p}f_{p}dp}[/math]
Notice that [math]f_{X}\left(x\right)[/math] does not depend on the random variable of [math]f\left(\left.p\right|x=1\right)[/math], which is [math]p[/math]. In fact, the denominator is only required to ensure that [math]f\left(\left.p\right|x=1\right)[/math] integrates to one.
The implication is that we can ignore the denominator and focus on the part that does depend on [math]p[/math], the kernel of [math]f_{\left.p\right|X}[/math]. We end up with the following identity:
[math]f\left(\left.p\right|X\right)\propto p^{\alpha}\left(1-p\right)^{\beta-1}[/math]
where [math]\propto[/math] can be read as “is proportional to”, and [math]p^{\alpha}\left(1-p\right)^{\beta-1}[/math] is the kernel.
Inspection of the Kernel implies that [math]f\left(\left.p\right|x=1\right)[/math] is a Beta distribution with parameters [math]\alpha+1[/math] and [math]\beta[/math].
The mean and variance of [math]\left.p\right|x=1[/math] are given by
[math]\begin{aligned} E\left(\left.p\right|x=1\right) & =\frac{\alpha+1}{\alpha+\beta+1}.\\ Var\left(\left.p\right|x=1\right) & =\frac{\left(\alpha+1\right)\beta}{\left(\alpha+\beta+1\right)^{2}\left(\alpha+\beta+2\right)}.\end{aligned}[/math]
It is often easy to identify the distribution by its kernel. In our example, it is clear that
[math]f_{X}\left(1\right)=\frac{\Gamma\left(\alpha+\beta\right)}{\Gamma\left(\alpha\right)\Gamma\left(\beta\right)}.\frac{\Gamma\left(\alpha+1\right)\Gamma\left(\beta\right)}{\Gamma\left(\alpha+\beta+1\right)}=\frac{\alpha}{\alpha+\beta},[/math]
so that we end up with a Beta distribution that integrates to one.
Conjugate Priors
You may have noticed that we started out with a Beta prior, and ended with a Beta posterior; the only difference between the distributions were the parameters.
In this case, we say that the Beta distribution is a conjugate prior with a Bernoulli likelihood, i.e., when using the Bernoulli likelihood, starting with a Beta prior will leads us to a Beta posterior. This is extremely convenient, since it allows us to simply update distribution parameters.
When this does not hold, one has to keep track of the whole posterior distribution, which typically gets more and more complicated as more data is fed into it. You can find a list of conjugate priors here.
Example: Normal Distribution
Let [math]\sigma^{2}[/math] be known, and
- Likelihood: [math]f_{\left.X\right|\mu}=N\left(\mu,1\right)[/math].
- Prior: [math]f_{\mu}=N\left(0,100\right)[/math].
Focusing on the Kernels, we know that
[math]\begin{aligned} f_{\left.\mu\right|X} & \propto\exp\left(-\frac{1}{2}\left(x-\mu\right)^{2}\right)\exp\left(-\frac{1}{2.100}\mu^{2}\right)\\ & =\exp\left\{ -\frac{1}{2}\left(x^{2}+\mu^{2}-2x\mu+\frac{\mu^{2}}{100}\right)\right\} \\ & \propto\exp\left\{ -\frac{1}{2}\left[\frac{101}{100}\left(\mu^{2}-2\mu\frac{100}{101}x+\left(\frac{100}{101}x\right)^{2}-\left(\frac{100}{101}x\right)^{2}\right)\right]\right\} \\ & \propto\exp\left\{ -\frac{\left(\mu-\frac{100}{101}x^{2}\right)}{2.\frac{100}{101}}\right\} \end{aligned}[/math]
Where the proportional signs keep track of expressions that depend solely on [math]x[/math] being added or removed from the exponential. Notice that we can multiply or divide the pdf by functions of [math]x[/math] at will, because [math]x[/math] does not belong to the kernel (after all, this is a pdf of [math]p[/math]). Instead, [math]x[/math] belongs to the normalizing constant. We already know that the posterior integrates to one, so our goal is to find the right kernel, and we can always adjust the constant later.
The result above implies that
[math]\begin{aligned} f_{\left.\mu\right|X} & \propto\exp\left\{ -\frac{\left(\mu-\frac{100}{101}x^{2}\right)}{2.\frac{100}{101}}\right\} \\ \Downarrow\\ f_{\left.\mu\right|X} & =N\left(\frac{100}{101}x^{2},\frac{100}{101}\right).\end{aligned}[/math]
The fact that we ended up with a normal distribution is a consequence of the fact that the normal distribution is a conjugate prior with a normal likelihood function.
"Counterexample"
Consider now a case where conjugate priors are not used.
- Likelihood: [math]f_{\left.X\right|\mu}=N\left(\mu,1\right)[/math]
- Prior: [math]f_{\mu}=Beta\left(4,5\right)[/math]
In this case,
[math]f_{\left.\mu\right|X}\propto f_{\left.X\right|\mu}.f_{\mu}=\exp\left(-\frac{1}{2}\left(x-\mu\right)^{2}\right)\mu^{3}\left(1-\mu\right)^{4}1\left(\mu\in\left(0,1\right)\right).[/math]
This expression is already complex for a single observation of [math]x[/math], and not similar to any classical distribution. As more observations are added, the expression of the posterior will complicate even further. On the other hand, when conjugate priors are used, only the parameters evolve. The use of conjugate priors will be clear in the next section.
Multiple Observations
In the normal case for a single observation, the following holds:
[math]\left.\begin{array}{c} f_{\left.X\right|\mu}=N\left(\mu,\sigma^{2}\right)\\ f_{\mu}=N\left(\mu_{0},\sigma_{0}^{2}\right) \end{array}\right\} \Rightarrow f_{\left.\mu\right|X}=N\left(\frac{\sigma_{0}^{2}}{\sigma^{2}+\sigma_{0}^{2}}x+\frac{\sigma^{2}}{\sigma^{2}+\sigma_{0}^{2}}\mu_{0},\left(\frac{1}{\sigma^{2}}+\frac{1}{\sigma_{0}^{2}}\right)^{-1}\right)[/math]
Notice the following results:
- The posterior mean is a weighted average of the prior mean [math]\mu_{0}[/math] and the data [math]x[/math].
- The posterior variance does not depend on [math]x[/math] (this is a property of the Normal).
- Estimation: A large [math]\sigma_{0}^{2}[/math] is often preferred.
- Setting [math]\sigma^{2}=\infty[/math] is possible (uninformative/improper prior) but not well-defined.
Finally, notice that this result can be used to provide a generalization for the case of multiple observations.
2 Observations
Note that
[math]\begin{aligned} f\left(\left.\mu\right|x_{1},x_{2}\right) & =\frac{f\left(\mu,x_{1},x_{2}\right)}{f\left(x_{1},x_{2}\right)}\\ & =\frac{f\left(\left.x_{1}\right|\mu,x_{2}\right)f\left(\left.x_{2}\right|\mu\right)f\left(\mu\right)}{fx_{1},x_{2}}\\ & =\frac{f\left(\left.x_{1}\right|\mu\right)f\left(\left.x_{2}\right|\mu\right)f\left(\mu\right)}{fx_{1},x_{2}}\\ & \propto f\left(\left.x_{1}\right|\mu\right)f\left(\left.x_{2}\right|\mu\right)f\left(\mu\right)\end{aligned}[/math]
where the last equality follows from the fact that the data is a random sample.
We can take advantage of this result by calculating [math]f\left(\left.\mu\right|x_{1},x_{2}\right)[/math] sequentially:
First, we calculate
[math]f_{\left.\mu\right|x_{1}}=f_{\left.x_{1}\right|,\mu}.f_{\mu}=N\left(\frac{\sigma_{0}^{2}}{\sigma^{2}+\sigma_{0}^{2}}x_{1}+\frac{\sigma^{2}}{\sigma^{2}+\sigma_{0}^{2}}\mu_{0},\left(\frac{1}{\sigma^{2}}+\frac{1}{\sigma_{0}^{2}}\right)^{-1}\right)[/math]
Then, we use the result, [math]f_{\left.\mu\right|x_{1},x_{2}}=f_{\left.x_{1}\right|,\mu}.f_{\mu}[/math] as the prior to update for [math]x_{2}[/math], i.e.,
[math]f_{\left.\mu\right|x_{1},x_{2}}\propto\underset{\text{likelihood}}{\underbrace{f_{\left.x_{2}\right|\mu}}}\underset{\text{prior}}{\underbrace{f_{\left.\mu\right|x_{1}}}}[/math]
s.t.
[math]f_{\left.\mu\right|x_{1},x_{2}}=N\left(\frac{\sigma_{0}^{2}}{\sigma^{2}+2\sigma_{0}^{2}}\left(x_{1}+x_{2}\right)+\frac{\sigma^{2}}{\sigma^{2}+2\sigma_{0}^{2}}\mu_{0},\left(\frac{2}{\sigma^{2}}+\frac{1}{\sigma_{0}^{2}}\right)^{-1}\right)[/math]
[math]n[/math] Observations
For [math]x_{1}..x_{n}[/math], it follows that
[math]f_{\left.\mu\right|x_{1}..x_{n}}=N\left(\frac{\sigma_{0}^{2}}{\sigma^{2}+n\sigma_{0}^{2}}\sum_{i=1}^{n}x_{i}+\frac{\sigma^{2}}{\sigma^{2}+n\sigma_{0}^{2}}\mu_{0},\left(\frac{n}{\sigma^{2}}+\frac{1}{\sigma_{0}^{2}}\right)^{-1}\right).[/math]
Notice that unlike in the previous example, the expression for the posterior distribution is "stable", even for a very high number of observations.
Theorem: Berstein von-Mises
Let [math]\widehat{\theta}_{B}[/math] be a point estimator for Bayesian inference (i.e., [math]\widehat{\theta}_{B}=E\left(\left.\theta\right|X\right)[/math]) and [math]\widehat{\theta}_{ML}[/math] be the MLE. Then,
[math]\sqrt{n}\left(\widehat{\theta}_{B}-\theta_{0}\right)\overset{d}{\rightarrow}N\left(0,I\left(\theta_{0}\right)^{-1}\right),\text{ where }\theta_{0}\text{ is the true value of }\theta.[/math]
and
[math]\sqrt{n}\left(\widehat{\theta}_{B}-\widehat{\theta}_{ML}\right)\overset{p}{\rightarrow}0[/math]
The second result is relatively striking: it tells us that even after scaling by [math]\sqrt{n}[/math], the ML and Bayes estimators converge in probability.
In practice, researchers can use an estimate of [math]I\left(\theta\right)^{-1}[/math] based on the variance implied by [math]f_{\left.\theta\right|X}[/math] for hypothesis testing. In relatively complicated cases, priors need not belong to conjugate families, in which case numerical methods are used, including taking draws from distributions via the Gibbs sampler and the Metropolis Hastings algorithm.