Full Lecture 13
Contents
Test Optimality (cont.)
Optimality for tests with simple null and alternative hypotheses has been established by the Neyman-Pearson lemma.
For one-sided tests, the Neyman-Pearson lemma is also useful:
Consider the testing problem [math]H_{0}:\theta=\theta_{0}[/math] vs. [math]H_{1}:\theta\gt \theta_{0}[/math]. We consider each value of the alternative hypothesis [math]\theta_{1}\gt \theta_{0}[/math]. Each value yields the simple test [math]H_{0}:\theta=\theta_{0}[/math] vs. [math]H_{1}^{*}:\theta=\theta_{1}[/math]. We then use the Neyman-Pearson lemma at each value of [math]\theta_{1}\gt \theta_{0}[/math]. If all values of [math]\theta_{1}[/math] yield the same UMP level [math]\alpha[/math] test, then we have found the unique UMP level [math]\alpha[/math] test.
The lemma implies that:
- If these tests coincide for all values of [math]\theta_{1}\gt \theta_{0}[/math], then the UMP test is [math]\frac{f\left(\left.x\right|\theta_{1}\right)}{f\left(\left.x\right|\theta_{0}\right)}\gt k[/math].
- If the tests do not coincide for all values of [math]\theta_{1}\gt \theta_{0}[/math], then no UMP level [math]\alpha[/math] test exists.
When we say that the tests coincide for all values of [math]\theta_{1}\gt \theta_{0}[/math], we mean that no matter the specific value of [math]\theta_{1}[/math], we will obtain the same exact test. This will be clearer with the following example.
Example: Normal
Suppose [math]X_{i}\overset{iid}{\sim}N\left(\mu,\sigma^{2}\right)[/math] where [math]\sigma^{2}[/math] is known. Let us derive the UMP level [math]\alpha[/math] test of
[math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu=\mu_{1}\gt \mu_{0}[/math] for a given [math]\mu_{1}[/math] at a time.
The Neyman-Pearson lemma suggests a test of the form [math]\frac{f\left(\left.x\right|\theta_{1}\right)}{f\left(\left.x\right|\theta_{0}\right)}\gt k[/math]. With some algebra, the left-hand side yields:
[math]\begin{aligned} \frac{\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left(-\sum_{i=1}^{n}\frac{\left(x_{i}-\mu_{1}\right)^{2}}{2\sigma^{2}}\right)}{\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left(-\sum_{i=1}^{n}\frac{\left(x_{i}-\mu_{0}\right)^{2}}{2\sigma^{2}}\right)} & =\exp\left(\sum_{i=1}^{n}\frac{\left(x_{i}-\mu_{0}\right)^{2}}{2\sigma^{2}}-\frac{\left(x_{i}-\mu_{1}\right)^{2}}{2\sigma^{2}}\right)\\ & =\exp\left(\frac{1}{2\sigma^{2}}\left(\sum_{i=1}^{n}x_{i}^{2}-2\mu_{0}x_{i}+\mu_{0}^{2}-\left(x_{i}^{2}-2\mu_{1}x_{i}+\mu_{1}^{2}\right)\right)\right)\\ & =\exp\left(\frac{1}{2\sigma^{2}}\left(\sum_{i=1}^{n}2x_{i}\left(\mu_{1}-\mu_{0}\right)+\mu_{0}^{2}-\mu_{1}^{2}\right)\right)\\ & =\exp\left(\frac{1}{2\sigma^{2}}\left(2n\overline{x}\left(\mu_{1}-\mu_{0}\right)+n\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}+\mu_{1}\right)\right)\right)\\ & =\exp\left(\frac{n\left(\mu_{1}-\mu_{0}\right)}{2\sigma^{2}}\left(2\overline{x}-\left(\mu_{0}+\mu_{1}\right)\right)\right)\end{aligned}[/math]
Going back to the original condition and solving it w.r.t. [math]\overline{x}[/math] yields “reject iff”:
[math]\begin{aligned} & \exp\left(\frac{n\left(\mu_{1}-\mu_{0}\right)}{2\sigma^{2}}\left(2\overline{x}-\left(\mu_{0}+\mu_{1}\right)\right)\right)\gt k\\ \Leftrightarrow & \overline{x}\gt \frac{1}{2}\left(\mu_{0}+\mu_{1}+\frac{2\sigma^{2}\log\left(k\right)}{n\left(\mu_{1}-\mu_{0}\right)}\right)\end{aligned}[/math]
Apparently, our test does depend on [math]\mu_{1}[/math], and so it does not seem UMP. However, we will now show that for different values of [math]\mu_{1}[/math], we will end up with the exact same test.
For example, let [math]\alpha=0.05[/math], [math]n=30[/math], [math]\sigma^{2}=1[/math], [math]\mu_{0}=0[/math] and [math]\mu_{1}=0.1[/math]. In this case, the probability of a type 1 error can be written as:
[math]\begin{aligned} Pr\left(\overline{X}\gt \underset{=k^{'}}{\underbrace{\frac{1}{2}\left(0+0.1+\frac{2\log\left(k\right)}{3}\right)}}\right) & =0.05\end{aligned}[/math]
Using the fact that [math]\overline{x}\sim N\left(\mu_{0},\frac{\sigma^{2}}{n}\right)[/math] and solving for [math]k[/math] is approximately equal to [math]2.12[/math], which yields [math]k^{'}=0.3[/math]. So, we will reject the null hypothesis if [math]\overline{x}\gt 0.3[/math]. This produces a level [math]\alpha[/math] test.
Now, suppose that [math]\mu_{1}=0.2[/math].
In this case, the probability of a type 1 error can be written as
[math]Pr\left(\overline{X}\gt \frac{1}{2}\left(0.2+\frac{2\log\left(k\right)}{6}\right)\right)=0.05[/math]
where [math]k[/math] now approximately equals [math]3.33[/math], while [math]k^{'}=0.3[/math] as before.
Our test turns out to be the same, independently of the value of [math]\mu_{1}[/math], i.e., the test does not depend on the value of [math]\mu_{1}[/math]. The intuition for the test not depending on the alternative hypothesis is that the critical value is set so that the test rejects the null, when [math]\mu=\mu_{0}[/math], [math]\alpha\% [/math] of the time. This test only depends on the null hypothesis; not on the alternative hypothesis: We can write our rejection decision as [math]\overline{x}\gt k^{'},[/math] where [math]k^{'}[/math] is whatever constant we need to set the intended probability of type 1 errors.
The Neyman-Pearson lemma states that the inequality above produces the unique UMP level [math]\alpha[/math] test, with a probability of a type 1 error equal to:
[math]\begin{aligned} & P_{\mu_{0}}\left(\overline{X}\gt k^{'}\right)=\alpha\\ \Leftrightarrow & 1-\Phi\left(\frac{\sqrt{n}\left(k^{'}-\mu_{0}\right)}{\sigma}\right)=\alpha.\end{aligned}[/math]
Karlin-Rubin Theorem
In some cases, it is straightforward to derive the UMP test.
The Karlin-Rubin theorem states that the UMP level [math]\alpha[/math] test exists for one-sided testing,
[math]H_{0}:\theta\leq\theta_{0}[/math] vs. [math]H_{1}:\theta\gt \theta_{0}[/math]
if [math]f\left(\left.X\right|\theta\right)[/math] belongs to the exponential family and [math]\omega\left(\theta\right)[/math] is monotone (i.e., the pdf/pmf satisfies the monotone likelihood ratio property).
In this case, we reject [math]H_{0}[/math] when [math]\sum_{i=1}^{n}t\left(X_{i}\right)[/math] is large.
2-sided tests
Consider now the testing problem [math]H_{0}:\theta=\theta_{0}vs.H_{1}:\theta\neq\theta_{0}[/math].
For values [math]\theta_{1}\gt \theta_{0}[/math], we have already seen that the UMP test rejects [math]H_{0}[/math] if [math]\overline{x}\lt k^{'}.[/math]
For values of [math]\theta_{1}\lt \theta_{0}[/math], it is easy to show that the Neyman-Pearson lemma yields a test that rejects [math]H_{0}[/math] if [math]\overline{x}\gt k^{'}.[/math]
Because the suggested UMP test depends on the values of [math]\theta_{1}[/math], the Neyman-Pearson lemma implies that there is a UMP [math]\alpha[/math]-level test does not exist (the lemma is written in the form of “if and only if”, such that if it does not yield a unique test, then a UMP test does not exist).
If one restricts the class of tests further, it is often possible to obtain (a more restricted type of) optimality. We will restrict ourselves to the class of unbiased tests.
Unbiased Tests
An unbiased test satisfies
[math]\text{sup}_{\theta\in\Theta_{0}}\,\beta\left(\theta\right)\leq\text{inf}_{\theta\in\Theta_{1}}\,\beta\left(\theta\right)[/math]
that is, the value of the power function in the null set is always below the value in the alternative set.
Unbiased tests are important because UMP unbiased (UMPU) tests often exist, even when unrestricted UMP tests do not.
A typical example is the case of [math]N\left(\mu,1\right)[/math], with [math]H_{0}:\mu=\mu_{0}vs.H_{1}:\mu\neq\mu_{0}.[/math]
(We will not go into the generalized Neyman-Pearson result applied to the optimal unbiased test.)
In the [math]N\left(\mu,1\right)[/math], it turns out that the UMPU is [math]T\left(X\right)=\left|\overline{X}\right|,[/math] i.e., we reject [math]H_{0}[/math] iff [math]\left|\overline{X}\right|\gt c.[/math]
Consider the following figure, which plots the power functions of the UMP one-sided tests (in orange and blue), and the power function of the two-sided of the UMPU test (in green).
All curves intersect 0.05 at [math]\mu=0[/math], the null hypothesis in this case.
The blue curve is the power function for UMP test [math]H_{0}:\mu=0[/math] vs. [math]H_{1}:\mu\gt 0[/math]: Notice it is relatively very likely to reject [math]H_{0}[/math] when [math]\mu\gt 0[/math].
The orange curve is the power function for UMP test [math]H_{0}:\mu=0[/math] vs. [math]H_{1}:\mu\lt 0[/math]: It is more likely to reject [math]H_{0}[/math] when [math]\mu\lt 0[/math].
Each of these power curves is unsuitable for test problem [math]H_{0}:\mu=0vs.H_{1}:\mu\neq0.[/math]
The green curve is the power function for the two-sided UMPU test. It does extremely well in the regions where the each of the one-sided power functions do the worst. However, notice that it doesn’t do as well where the other power functions do their best. This is expected, since the one-sided tests are UMP.
Intuitively, the two-sided test reallocates rejections by increasing the power function relative to the places where the one-sided tests do worst, at the expense of the cases where they do best.
p-value
Consider the test [math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\lt \mu_{0}[/math], that rejects [math]H_{0}[/math] if [math]\overline{x}\lt c.[/math]
Up to now, we have decided to reject [math]H_{0}[/math] by choosing [math]c[/math] to satisfy a given probability of type 1 error. Specifically, we have often selected
[math]c:\,P_{\mu_{0}}\left(\overline{X}\lt c\right)=.05.[/math]
Let's define critical value [math]c[/math] above that establishes a type 1 error probability of 5% as [math]c_{0.05}.[/math]
Now, suppose we replaced the generic critical value [math]c[/math] by the realized statistic in the data, [math]\overline{x}[/math]. In this case, the probability of committing a type 1 error when [math]c=\overline{x}[/math] can be written as
[math]P_{\mu_{0}}\left(\overline{X}\lt \overline{x}\right)[/math]
Why would we want to replace the critical value with the realization of the test statistic?
Consider what happens, for example, if we plugged in the realized value of [math]\overline{x}[/math], and obtained [math]P_{\mu_{0}}\left(\overline{X}\lt \overline{x}\right)=0.03.[/math] Clearly, this means that [math]\overline{x}\lt c_{0.05}[/math], and we should reject the null hypothesis. This is equivalent to comparing [math]P_{\mu_{0}}\left(\overline{X}\lt \overline{x}\right)=0.03[/math] to [math]P_{\mu_{0}}\left(\overline{X}\lt c_{0.05}\right)=0.05[/math], and noticing that we reject the null hypothesis as long as [math]P_{\mu_{0}}\left(\overline{X}\lt \overline{x}\right)\lt \alpha=0.05.[/math]
In other words, if the type 1 error probability associated with critical value [math]\overline{x}[/math] falls below the probability threshold [math]\alpha[/math], we reject the null hypothesis.
As you may have suspected, the p-value is a statistic. One advantage of using p-values is that we obtain a quantitative measure of “by how much our hypothesis was rejected.” For example, a p-value of [math]0.01[/math] provides more evidence against the null hypothesis than a p-value of [math]0.04.[/math]
We now provide a working definition of p-value (more formal and general definitions exist, for example for composite [math]H_{0}[/math]).
Definition
A p-value is the type 1 error probability of test statistic [math]T\left(X\right)[/math] with critical value [math]T\left(x\right)[/math], i.e.,
[math]p-value=P_{\theta_{0}}\left(T\left(X\right)\lt T\left(x\right)\right)[/math]
for the case where [math]T\left(X\right)\lt T\left(x\right)[/math] implies that [math]\theta_{0}[/math] is rejected.
Again, consider the test [math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\lt \mu_{0}[/math], that rejects [math]H_{0}[/math] if [math]\overline{x}\lt c.[/math]
We can calculate the p-value as:
[math]\begin{aligned} & P_{\mu_{0}}\left(\overline{X}\lt \overline{x}\right)\\ = & P_{\mu_{0}}\left(\underset{\sim N\left(0,1\right)}{\underbrace{\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}}}\lt \frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\right)\\ = & \Phi\left(\frac{\overline{x}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right).\end{aligned}[/math]
Some Notes: Notation, z-test, t-test
[math]z_{\alpha}[/math] Notation
If you haven’t mastered the previous content, this section will be very confusing. So, please, make sure you feel well grounded, because we will now discuss other common ways in which you will see hypothesis tests written for the case of parameter [math]\mu[/math] in the normal distribution.
Consider the test [math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\lt \mu_{0}[/math], that rejects [math]H_{0}[/math] if [math]\overline{x}\lt c.[/math]
As we have seen before, the probability of a type 1 error can be calculated as
[math]\begin{aligned} & P_{\mu_{0}}\left(\overline{X}\lt c\right)\\ = & P_{\mu_{0}}\left(\frac{\overline{X}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\lt \frac{c-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right)\\ = & P_{\mu_{0}}\left(Z\lt \frac{c-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right)\\ = & \Phi\left(\frac{\sqrt{n}\left(c-\mu_{0}\right)}{\sigma}\right).\end{aligned}[/math]
Above, we transformed [math]\overline{X}[/math] by subtracting its mean and dividing by its standard deviation, so that we obtain a random variable with distribution [math]N\left(0,1\right).[/math]
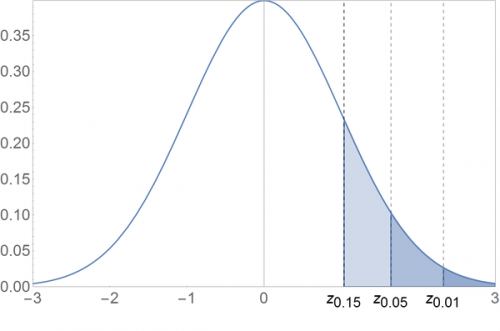
Let us define [math]z_{\alpha}[/math] implicitly, as the value of [math]z[/math] that satisfies [math]1-\Phi\left(z\right)=\alpha[/math], that is, [math]z_{\alpha}[/math] is a value s.t. a [math]N\left(0,1\right)[/math] random variable has [math]1-\alpha[/math] probability of being above it.
See the plot below for some examples:
Above, [math]z_{0.01}[/math] is given by [math]1-\Phi\left(z_{0.01}\right)=0.01\Leftrightarrow z_{0.01}=2.326[/math]. By the same procedure, [math]z_{0.05}=1.645[/math] and [math]z_{0.15}=1.036.[/math]
Also, notice that [math]z_{1-\alpha}[/math] is given by the value of [math]z[/math] that satisfies [math]\Phi\left(z\right)=\alpha[/math], and finally, because [math]N\left(0,1\right)[/math] is symmetric around zero, [math]z_{1-\alpha}=-z_{\alpha}.[/math]
Let us now solve
[math]\Phi\left(\frac{\sqrt{n}\left(c-\mu_{0}\right)}{\sigma}\right)=\alpha[/math]
with respect to [math]c.[/math]
Notice that this equality is satisfied if [math]\frac{\sqrt{n}\left(c-\mu_{0}\right)}{\sigma}=z_{1-\alpha}=-z_{\alpha}.[/math]
Solving this equation w.r.t. [math]c[/math] yields
[math]c=\mu_{0}-z_{\alpha}\frac{\sigma}{\sqrt{n}},[/math]
such that the probability of rejecting [math]H_{0}[/math] is indeed [math]\alpha.[/math]
Looking at this critical value, this means that we reject [math]H_{0}:\mu=0[/math] if
[math]\overline{X}\lt \mu_{0}-z_{\alpha}\frac{\sigma}{\sqrt{n}}.[/math]
This is an equivalent way of writing our test, which you will see in many textbooks.
The z-test: Using the Standardized Sample Mean as the Test (instead of the Sample Mean)
Up to now, we have mostly used [math]\overline{X}[/math] as the test statistic, when testing hypotheses about [math]\mu[/math], in the Normal context.
An alternative approach is to use the test statistic [math]Z=\frac{\overline{X}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}.[/math] This test statistic is the standardized sample mean, under the assumption that [math]\mu=\mu_{0}[/math].
This alternative statistic, often called the Z-score, can be useful. However, it is a priori less intuitive, because the test statistic involves a subtraction of [math]\mu[/math] under the null hypothesis. Why would we do this?
Let’s write the power function for the test:
[math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\lt \mu_{0},[/math]
using the [math]Z[/math] statistic:
[math]\beta\left(\mu\right)=P\left(reject\,H_{0}\right)=P\left(Z\lt c\right)=P\left(\frac{\overline{X}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\lt c\right).[/math]
We appear to have a bit of a problem: the power function is supposed to depend on [math]\mu[/math]. However, [math]\mu[/math] does not show up in the expression; only [math]\mu_{0}.[/math]
We can solve this by subtracting [math]\frac{\mu}{\frac{\sigma}{\sqrt{n}}}[/math] from both sides:
[math]Pr\left(\frac{\overline{X}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\lt c\right)=Pr\left(\frac{\overline{X}-\mu_{0}-\mu}{\frac{\sigma}{\sqrt{n}}}\lt c-\frac{\mu}{\frac{\sigma}{\sqrt{n}}}\right)=Pr\left(\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\lt c-\frac{\mu-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right).[/math]
Now, the left-hand size is distributed as a [math]N\left(0,1\right)[/math] r.v., such that
[math]\beta\left(\mu\right)=Pr\left(\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\lt c-\frac{\mu-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right)=\Phi\left(c-\frac{\mu-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right).[/math]
The use of statistic [math]Z[/math] appears to have yielded a slightly more complicated power function than we had when we used [math]\overline{X}[/math] directly as the test statistic. However, consider now the problem of setting [math]c[/math] to ensure the test is of level [math]\alpha[/math]:
[math]\begin{aligned} & \left.\Phi\left(c-\frac{\mu-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}\right)\right|_{\mu=\mu_{0}}=\alpha\\ \Leftrightarrow & \Phi\left(c\right)=\alpha\end{aligned}[/math]
such that we obtain the result that [math]c=-z_{\alpha}.[/math]
The benefit of using statistic [math]Z[/math] (usually denoted as [math]Z[/math]) is now clear: When we use statistic [math]Z=\frac{\overline{X}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}[/math], we simply need to compare the value of the transformed mean with [math]-z_{\alpha}.[/math] If [math]Z\lt -z_{\alpha}[/math], we reject the null hypothesis.
The t-test: Unknown Population Variance
In all of the normal examples, we have maintained that [math]\sigma^{2}[/math] is known. This is for simplification purposes, but it is hardly the case in general.
Consider the hypothesis test [math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\gt \mu_{0}[/math].
We have just seen that one way to write the decision rule, is to reject [math]H_{0}[/math] iff
[math]\begin{aligned} \Leftrightarrow Z= & \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\gt z_{\alpha}\end{aligned}[/math]
Now, suppose [math]\sigma[/math] is unknown. In this case, using the LRT, we would derive
[math]T_{LR}=2\left[\max_{\mu,\sigma}\,l\left(\mu,\sigma\right)-\max_{\sigma}\,l\left(\mu_{0},\sigma\right)\right][/math]
where the first term is the log-likelihood evaluated at the maximum-likelihood parameters, and the second term is the log-likelihood evaluated at the restricted maximum likelihood value of [math]\sigma[/math].
The maximizations will yield the following expressions for [math]\widehat{\sigma}_{ML}[/math] and [math]\widehat{\sigma}_{ML_{0}}[/math]:
[math]\begin{aligned} \widehat{\sigma}_{ML} & =\frac{1}{n}\sum_{i=1}^{n}\left(X_{i}-\widehat{\mu}_{ML}\right)^{2}=\frac{1}{n}\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}\\ \widehat{\sigma}_{ML_{0}} & =\frac{1}{n}\sum_{i=1}^{n}\left(X_{i}-\mu_{0}\right)^{2}\end{aligned}[/math]
Simplifying the LRT is tedious, but it yields the rejection rule
[math]T_{LR}=\frac{\overline{X}-\mu}{\frac{s}{\sqrt{n}}}[/math] where
[math]s=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}[/math]
It is possible to show that [math]T_{LR}[/math] follows a t-distribution, with pdf [math]f_{t}\left(\left.x\right|\nu\right)=\frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{x^{2}}{\nu}\right)^{-\frac{1+\nu}{2}}[/math] where parameter [math]\nu=n-1[/math] and [math]\Gamma\left(\cdot\right)[/math] is the Gamma function.
Interval Estimation/Confidence Intervals
In interval estimation, we would like to isolate plausible values of some parameter [math]\theta[/math].
Remember that in point estimation, we have attempted to find the “most plausible” value of [math]\theta[/math]. In hypothesis testing, we assigned [math]\theta[/math] to one of two subsets of [math]\Theta[/math]. In interval estimation, we produce an interval that is likely to contain the true parameter [math]\theta[/math].
Let [math]\Theta\subset\mathbb{R}[/math]. An interval estimator of [math]\theta[/math] is a random interval [math]\left[L\left(X_{1}..X_{n}\right),U\left(X_{1}..X_{n}\right)\right][/math] where [math]L\left(\cdot\right)[/math] and [math]U\left(\cdot\right)[/math] are statistics. We will use interval estimators and confidence intervals as synonymous. (This works well as long as we don't nitpick.)
- The coverage probability of the interval is the function (of [math]\theta[/math]): [math]P_{\theta}\left(L\left(X_{1}..X_{n}\right)\leq\theta\leq U\left(X_{1}..X_{n}\right)\right)[/math] where the subscript in [math]P_{\theta}[/math] stresses the fact that [math]\theta[/math] is a scalar and not a random variable.
- The confidence coefficient is [math]\text{inf}_{\theta\in\Theta}P_{\theta}\left(L\left(X_{1}..X_{n}\right)\leq\theta\leq U\left(X_{1}..X_{n}\right)\right)[/math] i.e., for all values of [math]\theta\in\Theta[/math], the confidence coefficient is the minimum of the coverage probabilities.
Example: Normal
Let [math]X_{i}\overset{iid}{\sim}N\left(\mu,\sigma^{2}\right)[/math], where [math]\sigma^{2}[/math] is known. The interval [math]\left[\overline{X}-1.96\frac{\sigma}{\sqrt{n}},\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right][/math] is a 95% confidence interval (i.e., it has a confidence coefficient of 95%) of [math]\mu[/math]. To see this, note that
[math]\begin{aligned} & P_{\mu}\left(\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\leq\mu\leq\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right)\\ = & P_{\mu}\left(-1.96\frac{\sigma}{\sqrt{n}}\leq\mu-\overline{X}\leq1.96\frac{\sigma}{\sqrt{n}}\right)\\ = & P_{\mu}\left(-1.96\frac{\sigma}{\sqrt{n}}\leq\overline{X}-\mu\leq1.96\frac{\sigma}{\sqrt{n}}\right)\\ = & P_{\mu}\left(-1.96\leq\underset{\sim N\left(0,1\right)}{\underbrace{\frac{\sqrt{n}\left(\overline{X}-\mu\right)}{\sigma}}}\leq1.96\right)\simeq0.95.\end{aligned}[/math]
Notice in this case that the coverage probability is equal to [math]0.95[/math] at all values of [math]\mu[/math], such that the confidence coefficient does not depend on [math]\mu.[/math]
A common way to obtain confidence intervals is to 'invert' tests.
For example, consider the two-sided [math]Z[/math]-test of [math]H_{0}:\mu=\mu_{0}[/math] vs. [math]H_{1}:\mu\neq\mu_{0}[/math], that rejects [math]H_{0}[/math] iff [math]\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\gt \mu_{0}\text{ or }\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\lt \mu_{0}.[/math]
Notice that the test accepts [math]H_{0}[/math] iff [math]\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\leq\mu_{0}\leq\overline{X}+1.96\frac{\sigma}{\sqrt{n}}.[/math]
The confidence interval [math]\left[\overline{X}-1.96\frac{\sigma}{\sqrt{n}},\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right][/math] consists of those values of [math]\mu_{0}[/math] for which the two-sided [math]z[/math]-test does not reject [math]H_{0}:\mu=\mu_{0}[/math]. In other words, there is a duality between 5% tests and 95% confidence intervals.
In general, we create a 95% confidence set for [math]\theta\in\Theta[/math] by including those values of [math]\theta_{0}[/math] for which a 5% test of [math]H_{0}:\theta=\theta_{0}[/math] does not reject.
Optimality
A confidence set is optimal iff it is obtained by inverting an optimal test. Because an optimal test minimizes the probability of type 2 errors (i.e., accepting the null hypothesis when the alternative hypothesis was correct), the corresponding optimal interval is optimal in the sense that it minimizes the likelihood of including values of [math]\mu\neq\mu_{0}[/math] in the confidence interval.