Full Lecture 11
Contents
Hypothesis Testing
The goal of hypothesis testing is to select a subset of the parameter space [math]\Theta[/math].
Set [math]\Theta[/math] is first partitioned into disjoint subsets, [math]\Theta_{0}[/math] and [math]\Theta_{1}[/math], where [math]\Theta_{1}=\Theta\backslash\Theta_{0}[/math].
Then, we decide on a rule for choosing between [math]\Theta_{0}[/math] and [math]\Theta_{1}[/math].
Some Terminology
- A hypothesis is a statement about [math]\theta[/math].
- Null Hypothesis: [math]H_{0}:\theta\in\Theta_{0}[/math].
- Alternative Hypothesis: [math]H_{1}:\theta\in\Theta_{1}[/math].
- Maintained Hypothesis: [math]H:[/math][math]\theta\in\Theta[/math].
The goal of hypothesis testing is to decide for the null or the alternative hypothesis. Throughout the procedure, the maintained hypothesis is assumed.
A typical formulation of a hypothesis test is: [math]H_{0}:\theta\in\Theta_{0}\,vs.\,H_{1}:\theta\in\Theta_{1}[/math]
Example: Normal
Suppose [math]X_{i}\overset{iid}{\sim}N\left(\mu,1\right)[/math], where [math]\mu\geq0[/math] (maintained hypothesis) is unknown. The aim is to test whether [math]\mu=0[/math].
Notice that we can write the problem down in two equivalent formulations:
[math]H_{0}:\mu=0\,vs.\,H_{1}:\mu\gt 0[/math]
or
[math]H_{0}:\mu\gt 0\,vs.\,H_{1}:\mu=0[/math]
It is usually easier to consider the hypothesis test with the simple null hypothesis. The null (alternative) hypothesis is simple if [math]\Theta_{0}[/math]([math]\Theta_{1}[/math]) is a singleton. Otherwise, it is composite.
Testing Procedure
Suppose [math]X_{1}..X_{n}[/math] is a random sample with a pmf/pdf [math]f\left(\left.\cdot\right|\theta\right)[/math] where [math]\theta\in\Theta[/math] is unknown. Consider the test
[math]H_{0}:\theta\in\Theta_{0}\,vs.\,H_{1}:\theta\in\Theta_{1}[/math]
A testing procedure is a rule for choosing between [math]H_{0}[/math] and [math]H_{1}.[/math]
For example, in the normal example above, if the data come out relatively low, then we may opt for hypothesis [math]\mu=0[/math]; whereas we may opt for the alternative hypothesis that [math]\mu\gt 0[/math] if the data are relatively high.
There is no obvious way how we should define the decision rule. However, for any rule, we can define a data region that corresponds to supporting one of the alternatives.
Let [math]C\subseteq\mathbb{R}^{n}[/math]. The rule "reject [math]H_{0}[/math] iff [math]\left(X_{1}..X_{n}\right)\in C[/math]" (i.e., if the data fall in the region) is a testing procedure with critical region [math]C[/math].
Example: Normal
Suppose [math]X_{i}\overset{iid}{\sim}N\left(\mu,1\right)[/math], where [math]\mu\geq0[/math] is unknown, and [math]H_{0}:\mu=0\,vs.\,H_{1}:\mu\gt 0.[/math]
A possible decision rule is to reject [math]H_{0}[/math] if [math]\overline{X}\gt 2[/math]. Of course, we could have selected a different right-hand side, like 3, or even a function of [math]n[/math] to account for the fact that higher samples produce more precise means.
For our current example, the critical region is given by [math]C=\left\{ \left(X_{1}..X_{n}\right)^{'}:\frac{\sum_{i=1}^{n}X_{i}}{n}\gt 2\right\}[/math].
- We call [math]\frac{\sum_{i=1}^{n}X_{i}}{n}[/math] the test-statistic: It’s a statistic that will be used to decide the test result.
- We call [math]2[/math] the test threshold or the critical value.
- One can practically always write tests as [math]T\left(X\right)\gt c[/math].
Hypothesis testing involves choosing a test statistic (left-hand side) and a critical value (right-hand side). Depending on the data, the condition is either satisfied or not (so, a test produces a binary outcome).
We will first discuss critical value selection (for generic tests or specific ones). I.e., we will focus on the right-hand side. In the next lecture, we discuss test selection.
But before we get in too deep, something completely different.
Variation on the Theme
Let’s stop for a second, and ask “why are we even doing this”? Why is it so important to determine whether [math]\mu=0[/math] or [math]\mu\gt 0[/math]? Why not simply estimate [math]\mu[/math] through maximum likelihood or the method of moments, and use whatever information we obtained? If we estimate [math]\mu=0.3[/math], well, then maybe [math]\mu[/math] is indeed 0.3 for all we know.
The debate about hypothesis testing dates back to the early to 20th century primarily between Ronald Fisher and Jerzy Neyman and continued for several decades. A significant part of the debate was philosophical. What we teach and study today is a product of that debate, taking mostly Neyman’s as well as his co-author Karl Pearson’s approach, but still informed by ideas from Ronald Fisher. Fisher’s motivation was in part whether to maintain or reject a currently-held scientific hypothesis. If the data disagreed with the current hypothesis sufficiently - in some formal way - then one could do away with it. In contrast, Neyman and Pearson’s approach pitches two hypotheses, and favors one or the other.
Over time, Neyman and Pearson’s approach gained momentum, probably due to the amount of formal tools used, as well as due to the Neyman-Pearson lemma, which establishes a form of optimality when selecting a test. The approach is agnostic in terms of the scientific method. In practice though, natural sciences employ this method conservatively: A current theory is disproved if - statistically speaking - the chance that the observations from an experiment disagreed simply because of randomness are very very small; yet, we we observe a disagreement in the data. (For example, our theory predicted that the chances of observing a sample mean higher than 0 was 0.00001%; yet we observed it.)
In the social sciences, there exists a mild debate about how conservative hypothesis testing should be. Because humans are so volatile, data about their behavior is not always good enough to convincingly disprove a theory. And clearly, social sciences face challenges in replicating experiments while keeping conditions completely stable. So, some authors have proposed that the dichotomous approach of lending support to one theory or another by partitioning the parameter space into two is inadequate for the social sciences. Instead, researchers should keep track of the parameters estimated over time, in different studies and experiments, and use full information instead.
Some related debates still take place: For example, does the dichotomous approach provide too much freedom/incentive for scientists to interfere with experimental results?
The point of this section is to try to sensitize you to the fact that, despite its mathematical language, hypothesis testing is a tool that does the job your ask of it. By studying it and understanding it well, you will be able to decide whether it solves the particular problem you face, whether it needs a tweak or two, or whether it is completely inapplicable/inappropriate.
Keep in mind though, that the theory is intricate and sometimes deceiving. The people I’ve talked to who know the most in the world about this area of statistics say as much. You may also want to keep in mind that many people know only a bit about it, yet will speak as if they were experts.
With that, let’s proceed into the jewel of the modern scientific method.
Type 1 and Type 2 Errors
The critical value is a fundamental aspect of hypothesis testing. In the previous normal example, we chose a critical value of [math]2[/math]. Was this a good idea? Surely the probability of selecting the right hypothesis is not 100% either way.
For any critical value, there will be cases where we will say that [math]\mu=0[/math] when in reality [math]\mu\gt 0[/math], and the converse will also happen. If we were always able to pick the right hypothesis, then there would be no uncertainty.
Let us first organize the possible cases of “hit and miss” in the following table:
| Truth\Decision | [math]H_{0}[/math] | [math]H_{1}[/math] |
| [math]H_{0}[/math] | [math]\unicode{x2714}[/math] | Type 1 error |
| [math]H_{1}[/math] | Type 2 error | [math]\unicode{x2714}[/math] |
The main diagonal is simple to memorize: If [math]H_{0}[/math] is true and we opt for [math]H_{0}[/math] (or if [math]H_{1}[/math] is true and... you get the point), then no errors were made. If we decide for [math]H_{1}[/math] when [math]H_{0}[/math] is true, then we have committed a type 1 error. If we decide for [math]H_{0}[/math] when [math]H_{1}[/math] is true, then we committed a type 2 error.
Example: Normal
Let’s use the normal example from before. After all, we need to get used to these relatively artificial error names.
In our example,
[math]H_{0}:\mu=0[/math] and [math]H_{1}:\mu\gt 0[/math].
- If we reject [math]\mu=0[/math] when it was true, then we commit a type 1 error.
- If we accept [math]\mu=0[/math] and it was false, then we commit a type 2 error.
So, provided an error was made, type 1 error happens when rejecting the null, type 2 error occurs when accepting the null. Rehearse this: Type 1 error, reject the null.... Type 1 error, reject the null...
Often, we select the critical value so that [math]P_{\theta_{0}}\left(\text{type 1 error}\right)\leq5\%[/math]. One interpretation typical in sciences is that we would like to be conservative, and only rarely reject the null hypothesis erroneously.
The 5% threshold used above is arbitrary. For example, in the natural sciences where experiments can be reproduced with high precision, we may use [math]p=0.003[/math] or even lower.
We will talk about the probability of committing a type 2 error in the next lecture. As a preview, we will minimize that probability, constrained by the fact that the probability of a type 1 error cannot surpass 5% (or some other established level).
An incredibly useful too to analyze this problem further is the power function (and then some graphs).
A Quick Note on Notation
Statements like [math]P_{\theta_{0}}\left(\text{type 1 error}\right)\leq5\%[/math] will be frequent from here on.
When using the subscript notation [math]P_{\theta_{0}}\left(\cdot\right)[/math], it may appear that we mean [math]P\left(\cdot|\theta=\theta_{0}\right)[/math]. The issue with this statement is that we do not consider [math]\theta[/math] to be a random variable (rather, it is the true value of the parameter, a constant), so it does not make sense to condition on it. Hence, the use of the subscript notation.
Power Function
The power function of a test with critical region [math]C[/math] is the function [math]\beta:\Theta\rightarrow\left[0,1\right][/math] given by
[math]\beta\left(\theta\right)=P_{\theta}\left[\left(X_{1}..X_{n}\right)'\in C\right]=P_{\theta}\left(\text{reject }H_{0}\right),\theta\in\Theta.[/math]
So, the power function returns a probability. It is super convenient because it summarizes type 1 and type 2 errors in a single function.
To see this, note that
[math]\begin{aligned} P_{\theta}\left(\text{type 1 error}\right) & =\beta\left(\theta\right),\,\theta\in\Theta_{0}\\ P_{\theta}\left(\text{type 2 error}\right) & =1-\beta\left(\theta\right),\,\theta\in\Theta_{1}\end{aligned}[/math]
From here on, we will work with examples.
Example 1: Normal
Let [math]X_{i}\overset{iid}{\sim}N\left(\mu,1\right)[/math], and consider the test
[math]H_{0}:\mu=0\,vs.\,H_{1}:\mu\gt 0[/math],
where the maintained hypothesis is [math]\mu\in\left[0,\infty\right)[/math].
Suppose we decide to reject [math]H_{0}[/math] if [math]\overline{X}\gt 0[/math] (i.e., the critical value is 0). We’ll discuss whether this is a sensible rule later.
The power function is given by
[math]\beta\left(\theta\right)=P_{\theta}\left(\text{reject }H_{0}\right),\theta\in\Theta[/math].
Since we know that [math]\overline{X}\sim N\left(\mu,\frac{1}{n}\right)[/math], we can further write
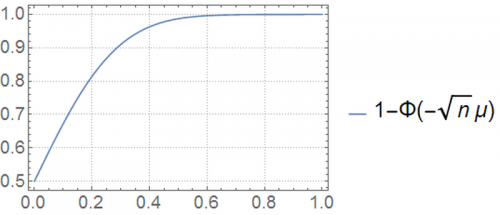
[math]\beta\left(\theta\right)=P_{\mu}\left(\text{reject }H_{0}\right)=P_{\mu}\left(\overline{X}\gt 0\right)=1-P_{\mu}\left(\overline{X}\leq0\right)=1-F_{\overline{X},\mu}\left(0\right)=1-\Phi\left(\frac{0-\mu}{\sqrt{\frac{1}{n}}}\right)=1-\Phi\left(-\sqrt{n}\mu\right)[/math].
Because we know that
[math]\begin{aligned} P_{\theta}\left(\text{type 1 error}\right) & =\beta\left(\theta\right),\,\theta\in\Theta_{0}\\ P_{\theta}\left(\text{type 2 error}\right) & =1-\beta\left(\theta\right),\,\theta\in\Theta_{1}\end{aligned}[/math]
It follows that (with a bit of abuse of notation)
[math]P_{\mu}\left(\text{type 1 error}\right)=\beta\left(\mu=\mu_0\right)=1-\Phi\left(-\sqrt{n}0\right)=50\%.[/math]
[math]P_{\mu}\left(\text{type 2 error}\right)=1-\beta\left(\mu\gt \mu_0\right)=1-\left(1-\Phi\left(-\sqrt{n}\mu\right)\right) = \Phi\left(-\sqrt{n}\mu\right)\text{ for }\mu\gt \mu_{0}[/math].
Let’s plot this power function, for [math]n=20[/math], as a function of the parameter of interest, [math]\mu[/math]:
Under the null hypothesis, [math]\mu=0[/math]. In this case, the probability of committing a type 1 error is [math]50\%[/math]. This means that if we repeated this exact experiment many times with [math]\mu=0[/math], and drew multiple values of [math]\overline{x}[/math] each time, our rule would have rejected the null hypothesis approximately 50% of the time.
Is this surprising? The magical 50% figure is a consequence of the chosen test statistic and the cutoff of zero of our admittedly arbitrary rule. The random variable of interest in our test (i.e., our test statistic) is the sample mean. We obtained this result because a [math]N\left(0,1\right)[/math] produces sample means (each calculated with [math]n=20[/math]) above zero 50% of the time. Whether this rejection rate of the null hypothesis is appropriate depends on the application.
What does the power function tell us?
It tells us the probability of rejecting [math]H_{0}[/math] when [math]\mu=0[/math], according to our rule. At [math]H_{1}[/math] ([math]\mu\gt 0[/math]), it gives us one minus the probability of committing a type 2 error. In other words, at [math]\mu\gt 0[/math], it tells us the probability of accepting the alternative hypothesis when it was indeed correct, for each specific value of [math]\mu[/math].
We would like to produce a power function that equals zero at [math]\mu=0[/math], and equals 1 at [math]\mu\gt 1[/math]. However, as long as [math]\overline{X}[/math] is uncertain, we cannot ensure this.
Intuitively, we want to minimize the power function at the null set, and maximize it at the alternative set.
Setting the Critical Value
Suppose we would like the probability of a type 1 error to equal 5% exactly. The way to do this is start with some fictitious threshold [math]c[/math], write down the probability of a type 1 error, and then equal it to 5% and solve w.r.t. [math]c[/math].
We rewrite our rule to reject [math]H_{0}[/math] when [math]\overline{X}\gt c[/math].
Then, [math]P_{\mu}\left(\text{type 1 error}\right)=P_{\mu}\left(\overline{X}\gt c\right)=1-P_{\mu}\left(\overline{X}\leq c\right)=1-\Phi\left(\frac{c-\mu}{\sqrt{\frac{1}{n}}}\right)[/math].
Under the null hypothesis that [math]\mu=0[/math], and for [math]n=20[/math], we want [math]P_{\mu}\left(\text{type 1 error}\right)=1-\Phi\left(c\sqrt{20}\right)=0.05[/math]. This equation does not admit a closed form solution, but the approximate numerical solution is [math]c\simeq0.368[/math].
At this value, [math]P_{\mu}\left(\text{type 1 error}\right)=0.05[/math].
Is it intuitive that as we increase the critical value (from zero in the previous example to 0.368 in this one), the probability of a type 1 error decreases (from 50% to 5%).
First, fix [math]\mu=0[/math], and imagine drawing multiple sample means. Clearly, fewer of them fall above [math]c=0.368[/math] than above [math]c=0[/math]. Given that we reject [math]H_{0}[/math] when [math]\overline{X}\gt c[/math], the likelihood of rejection decreases as [math]c[/math] decreases. With [math]n=20,[/math] at [math]c=0.368[/math], it is exactly 0.05.
A note on [math]n[/math]
You may feel a bit uncomfortable about the fact that we fixed [math]n[/math] in these examples. Clearly, [math]n[/math] affects the choice of critical value to use. For example, if [math]n[/math] were very high, a very small deviation from zero could already justify rejecting the null hypothesis.
When [math]n[/math] is given, this is not an issue. However, when the researcher has the ability to set [math]n[/math], then she has two degrees of freedom, [math]c[/math] and [math]n[/math]. This can be useful in experimental design and data collection. If one has good information about [math]\sigma^{2}[/math], one may select [math]c[/math] and [math]n[/math] to determine the probability of a type 1 error, and the probability of a type 2 error simultaneously (at specific values of [math]\mu[/math]), for example, since it will be possible to create a system of equations with two unknowns.
Composite [math]H_{0}[/math]
We could have designed a test with a composite null hypothesis. In this case, we could select [math]c[/math] for example by solving problem
[math]\begin{aligned} \max_{c\in\mathbb{R},\mu\in\Theta_{0}} & \,P_{\mu}\left(\overline{X}\gt c\right)\\ s.t. & P_{\mu}\left(\overline{X}\gt c\right)\leq0.05,\end{aligned}[/math]
where
[math]\Theta_{0}[/math] is the set of [math]\mu[/math]’s contemplated in the null hypothesis.
However, designing a test with a simple null hypothesis is simpler, because we require equality to the specified rejection probability at a single value of [math]\mu[/math].